Lorsque vous cherchez à établir un secret partagé entre deux correspondants, le protocole d’échange de clés Diffie-Hellman est un incontournable. Il est « simple à mettre en œuvre » et permet de sécuriser des sessions de communications en garantissant la confidentialité persistante.

Comme toute la cryptographie moderne, la définition de ce protocole utilise des théories mathématiques. Dans notre cas, les groupes, la notion de générateur, d’exponentiation et de calcul de logarithme discret. Lorsque vous comprenez ces notions, le protocole est relativement facile à comprendre.

Pour faciliter sa compréhension, la plupart des auteurs utilisent une métaphore où les participants s’échangent de la peinture. Sans la couche de mathématiques, le protocole est encore plus facile à comprendre.

Voyons donc comment il fonctionne avec de la peinture et jusqu’où il fonctionne…

La métaphore des couleurs

Pour communiquer, Alice et Bob vont donc devoir établir un secret partagé et, comme vous vous en doutez, ce sera une couleur. Cette nuance particulière, appelons-là pour l’instant ■ taupe, ne sera connue que d’eux seuls.

Gris Taupe : comme tout le monde le sait, à force de mélanger des couleurs, on obtient toujours une sorte de ■ brun très moche et indéfinissable que n’importe quel enfant appelle ■ caca mais que les décorateurs d’intérieur ont décidé d’appeler ■ taupe.

Alice et Bob commencent par utiliser une première peinture commune. Comme tout se fait publiquement, n’importe qui peut voir cette couleur, i.e. Eve qui aimerait bien pouvoir connaître leur secrets. Prenons du ■ glauque.

Glauque : Sorte de ■ vert un peu ■ grisâtre tirant vers le ■ bleu canard. Personne n’est vraiment d’accord sur la nuance de couleur exacte. On peut partir du principe que, par sécurité, Alice a envoyé un échantillon à Bob.

Alice et Bob vont maintenant choisir chacun une autre couleur secrète. Après maintes hésitations, Alice s’arrête sur de l’■ amarante. Bob à choisi du ■ bleu depuis bien longtemps.

Amarante : Nuance de ■ pourpre qui évoque la fleur d’amarante. Bob appelle ça du ■ rose voir du ■ bordeaux dans ses grands jours mais il fallait une couleur commençant par A.

Bleu : Alice aurait dit ■ azur mais ça n’est pas vraiment la même couleur et, surtout, ça ne commence pas par B.

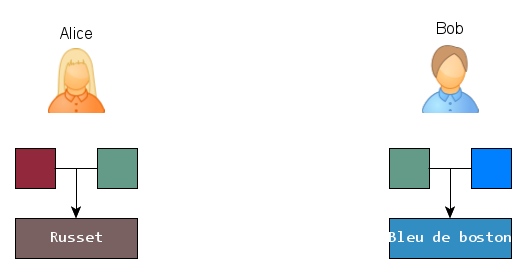
Chacun de leur côté, ils vont mélanger, à volumes égaux, un peu de leur couleur avec la couleur commune et s’envoyer une moitié de leur résultat. Cette couleur, envoyée publiquement est leur clé publique. Alice envoie une sorte de ■ russett et Bob lui retourne une nuance de ■ bleu de Boston.

Ils vont alors mélanger la couleur reçue avec leur couleur secrète pour obtenir le même mélange des trois couleurs à proportions égales. Ici, on obtient un ■ bleu kashmir.

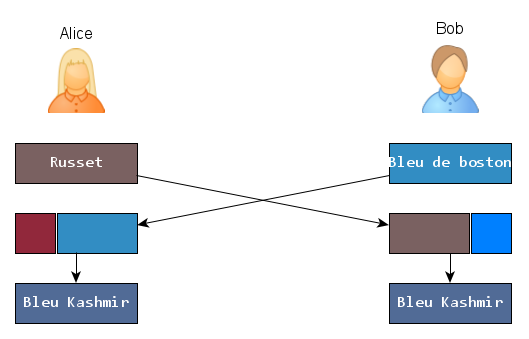
Bleu Kashmir : sorte de ■ bleu acier. On sent bien la parenté avec du ■ gris taupe mais comme dirait Bob, ça reste quand même bien Bleu tout ça.

La sécurité repose sur le fait qu’il est difficile pour Eve de trouver quelle est la nuance de gris taupe exacte en n’ayant observé que la couleur commune et les deux mélanges intermédiaires.

C’est ce qu’on appelle une « attaque sur Diffie Hellman ». Pour y arriver, il faudrait que Eve puisse enlever une portion de couleur commune (glauque) au mélange.

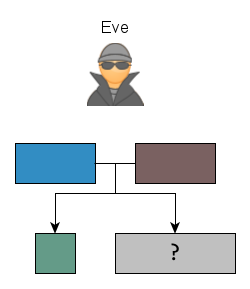
Métaphoriquement, « l’attaque sur le logarithme discret » consisterait à retrouver les couleurs privées à partir des couleurs publiques. Intuitivement, on sent que c’est à peut près la même difficulté.

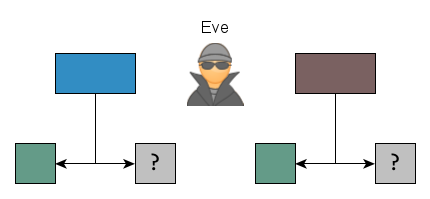
Et comme tout le monde le sait : une fois qu’on a commencé à mélanger les pinceaux, on ne retrouve jamais les couleurs d’origine.

La métaphore en vrai

Parmi les modélisation des couleurs possibles, nous avons choisi le triplet de couleurs primaires $(r, g, b)$ auxquels nous ajoutons un quatrième membre pour la quantité. Le code suivant est une implémentation en C++ d’exemple.

class Color
{
public:
    float r ;
    float g ;
    float b ;
    float w ;

public:

    Color(float r, float g, float b, float w = 1.0)
    : r(r), g(g), b(b), w(w)
    { }

    Color(std::string const & hex)
    {
        unsigned int r, g, b ;
        sscanf(hex.c_str(), "#%02x%02x%02x", &r, &g, &b) ;

        this->r = r / 256.0 ;
        this->g = g / 256.0 ;
        this->b = b / 256.0 ;
        this->w = 1.0 ;
    }
} ;

Le triplet $(r, g, b)$ peut s’assimiler à une quantité de pigments dans l’échantillon, pour connaître la nuance, il faut donc canoniser ces valeurs en divisant par la quantité ; principe similaire aux coordonnées homogènes. On peut utiliser cette opération pour écrire la couleur sur un flux de sortie :

template <typename Stream>
Stream & operator<<(Stream & stream, Color const & c)
{
    char buf[8] ;
    snprintf(buf, sizeof(buf), "#%02x%02x%02x",
        (unsigned int) (256.0 * c.r / c.w),
        (unsigned int) (256.0 * c.g / c.w),
        (unsigned int) (256.0 * c.b / c.w)
    ) ;
        
    stream << buf;
    return stream ;
}

Avec cette convention, les calculs de mélanges sont beaucoup plus simples, ajouter deux couleurs consiste simplement à ajouter les pigments et les quantités. On peut également définir un opérateur pour multiplier une couleur par un coefficient.

Color operator+(Color const & lhs, Color const & rhs)
{
    return Color(
        lhs.r + rhs.r,
        lhs.g + rhs.g,
        lhs.b + rhs.b,
        lhs.w + rhs.w
    ) ;
}

Color operator*(float f, Color const & rhs)
{
    return Color(
        f * rhs.r,
        f * rhs.g,
        f * rhs.b,
        f * rhs.w
    ) ;
}

L’ensemble de quadruplets possibles forme un groupe dans $(R^4, +)$. Notre modélisation à base de nombres à virgule flottante est un sous-ensemble qui, à quelques imprécisions de mesures près, formerait un groupe aussi.

Par contre, l’ensemble des couleurs qui ont un sens physique et réel forme un Quasigroupe. Pour que les valeurs décrivent une couleur, tous les nombres doivent être positifs et aucun pigment ne peut être supérieur à la quantité.

Dans un quasigroupe, cette opération de mélange perd donc la notion d’inverse : aucune couleur ne peut en annuler une autre. Le protocole d’échange de clés est alors parfaitement sûr puisqu’il est impossible pour Eve de retrouver les couleurs d’origine.

Mais ce n’est pas parce que Alice et Bob ont une convention (rester dans le monde réel des quasigroupe) que Eve est tenue de la respecter.

Pour son attaque, Eve peut tout à fait considérer des couleurs irrationnelles (pigments négatifs ou supérieur au poids) et ainsi faire ses calculs dans $(R^4, +)$, où inverser une couleur est possible (et même très simple) :

Color operator-(Color const & rhs)
{
    return -1.0 * rhs ;
}

Eve peut donc très facilement retrouver la couleur commune d’Alice et Bob. En mélangeant les couleurs publiques, elle obtient un mélange constitué d’une part de couleur secrète d’Alice, une part de celle de Bob et deux parts de la couleur initiale. En supprimant une part de couleur publique, elle obtiendra un mélange des trois couleurs à part égale.

Color getCommonSecret(
    Color const & base,
    Color const & pubA,
    Color const & pubB
    )
{
    return pubA + pubB - base ;
}

Il s’agit ici d’une attaque directe sur le problème de Diffie-Hellman. Eve calcule le secret partagé directement à partir des informations publiques, sans passer par les clés secrètes.

Le calcul de ces clés secrètes, c’est à dire de l’équivalent métaphorique du logarithme discrêt est également très facile à effectuer. En voici une implémentation :

Color log(
    Color const & base,
    Color const & pub,
    )
{
    return pub - base ;
}

On peut difficilement faire plus simple comme attaque.

Et après ?

Cette métaphore est adaptée pour illustrer l’idée que, si on dispose d’une opération difficilement inversible comme le mélange de pots de peinture, on peut définir un protocole pour établir un secret partagé. Notre expérience nous a appris qu’on ne peut pas physiquement annuler un mélange de couleur, nous comprenons et acceptons donc intuitivement la sécurité du protocole.

Mais ce n’est pas parce que quelque chose est physiquement impossible qu’on ne peut pas le modéliser, construire un modèle mathématique et, in fine, y faire des calculs utiles.

Les nombres complexes en sont un exemple. On sait tous que l’aire d’une figure ne peut pas être négative ! Mais on peut quand même imaginer une longueur de côté $i$ dont l’aire du carré soit -1. On peut alors l’utiliser pour construire un ensemble cohérent et découvrir la plus belle formule et tracer le plus bel ensemble.

Et ceci nous amène à un principe philosophique plus profond, en sécurité informatique mais pas que, le doute. Ce n’est pas parce qu’un protocole ou un algorithme nous paraissent intuitivement sûrs qu’ils le sont forcément :

Si on implémentait l’algorithme avec des couleurs, on penserait à un algorithme parfaitement sur alors qu’il serait facile à casser. Heureusement, on l’implémente plutôt avec des exponentiation modulaires d’entiers et plus récemment des courbes elliptiques qui, toutes deux, sont bien plus sûres.