COVID-19, Probabilités et Inférence Bayésienne
Divulgâchage : À force de voir des statistiques et des interprétations farfelues sur le COVID-19, je me suis dit que des explications sur les probabilités serait intéressantes pour mieux comprendre le sens de ces chiffres et vous parler d'Inférence Bayésienne vous permettrait d'en sortir des conclusions plus intéressantes.
Il y a quelques années, j’ai eu la chance de remplacer un professeur de maths au collège. Pendant deux semaines, j’ai tenté d’enseigner à des élèves de 4ème et 3ème l’intérêt des mathématiques. Ce fut difficile, et j’échouai lamentablement…
Plus tard, je veux juste être carreleur, ça me sert à rien les math !
Ils sont maintenant majeurs et en plein de crise de COVID-19, doivent être complètements perdus devant les statistiques publiées régulièrement. Comme ils ne savent pas démêler le vrai du faux, ils s’en remettent sûrement à leur intuition et adhèrent aux théories qui les arrangent le plus…

Même si je pense qu’aucun de mes élèves ne suit le [merveilleux] site des arsouyes, j’aimerais prendre un moment pour démystifier la notion de probabilité conditionnelle en décortiquant quelques statistiques sur le COVID-19.
Pour les données, je vais partir du point épidémiologique hebdomadaire de Santé publique France concernant l’épidémie de COVID19, celui du 2 avril 2020 (avec les données jusqu’au 31/03/2020) pour être exact.
Hospitalisations par âge
On va donc commencer par un exemple simple histoire de se faire la main.
Fréquence et probabilités
Si vous vous inquiétez des risques d’être atteint du COVID-19 au point d’être hospitalisé, vous pourriez regarder le tableau 2 (page 7), qui donne, au 31 mars 2020, le nombre d’hospitalisations par tranche d’âge, ainsi que leur proportion en pourcentage. Ces données sont reproduites ici :
| Classe d’âge | Hospitalisations | Proportion |
|---|---|---|
| 0-14 | 81 | 1 % |
| 15-44 | 1799 | 8 % |
| 45-64 | 6811 | 30 % |
| 65-74 | 5479 | 25 % |
| 75+ | 8241 | 37 % |
| Total | 22411 | 100 % |
J’ai volontairement ajouté la dernière ligne, total, pour vous montrer sur quoi porte ce pourcentage. Il s’agit de la proportion d’hospitalisations d’une tranche d’âge par rapport à l’ensemble des hospitalisations.
Mathématiquement, on parle de fréquence d’un événement (un malade a son âge dans un intervalle). Comme ces nombres sont conséquents, on peut également parler de la probabilité conditionnelle qu’un individu choisi au hasard ait son âge dans tel intervalle (événement noté ) sachant qu’il est hospitalisé pour COVID-19 (événement noté ) . Cette probabilité s’écrit et se calcule par la formule suivante : Soit le nombre d’hospitalisations de cet âge rapporté au nombre d’hospitalisations.
En lisant le tableau précédent, on peut rapidement faire le même genre de constatations que la presse :
- Plus d’une hospitalisation sur 3 a plus de 75 ans,
- Près de deux tiers des malades ont moins plus 65 ans,
- Une hospitalisation sur 10 concerne un moins de 45 ans.
Erreur d’interprétation
Le problème, c’est que même si ces phrases sont vraies, elle ne nous apportent pas l’information qu’on cherchait ; le risque, pour nous, d’être hospitalisé. Pour le trouver, il est tentant d’inférer avec les données dont on dispose et d’en tirer les mauvaises conclusions :
- Après 75 ans, on a une chance sur 3 d’être hospitalisé.

Mathématiquement, ce qu’on cherche, c’est la probabilité d’être hospitalisé () sachant que notre âge est dans un intervalle (), soit , la condition est en sens inverse par rapport à tout à l’heure et ça a toute son importance : Ces deux probabilités ne sont pas égales, on ne divise pas avec la même population.
Heureusement, on peut quand même passer de l’une à l’autre, avec de l’Inférence Bayésienne. Je pourrais écrire un article complet sur cette technique tellement elle est chouette mais pour aujourd’hui, retenez simplement cette équation :
Pour inverser la condition, il faut prendre en compte des facteurs supplémentaires, et .
Cette erreur de raisonnement est due à plusieurs biais cognitifs connus. Le biais d’appariement qui nous pousse à chercher une réponse en n’utilisant que les éléments qu’on a sous les yeux. Et réciproquement l’oubli de la fréquence de base qui nous occulte ces probabilités individuelles. En ne regardant que les fréquence au sein de hospitalisations, on se trompe.
Calcul du risque
Le risque qu’on veut calculer est en fait le rapport du nombre de personnes qui sont hospitalisées et la population totale. Pour une une classe d’âge, c’est le nombre d’hospitalisation de cette classe par rapport à la population de cette classe. On obtiens alors ce qu’on appelle l’incidence du phénomène, soit sa fréquence au sein de la population.
Mathématiquement, on pourrait bien sûr faire de l’Inférence Bayésienne, mais ici, il sera plus facile de calculer directement la probabilité :
Pour les données, je me tourne maintenant vers l’INSEE qui recense la population et publie régulièrement la pyramide des ages (et les données brutes si vous voulez faire vos propres calculs). Ainsi, nous disposons du nombre de personnes vivants en France répartie pour chaque année de naissance (et donc par âge).
Tourisme : Les centenaires sont par contre regroupés en une seule catégorie et représentés dans la barre au sommet de la pyramide.
Après avoir additionné les populations pour chacune des 5 classes d’âge, on peut calculer l’incidence du COVID-19 dans chaque groupe de population. Les données sont dans le tableau suivant (notez que l’incidence est exprimée « pour 100 000 »).
| Age | Population | Hospitalisation | Incidence / 100000 |
|---|---|---|---|
| 0-14 | 11943747 | 81 | 0,7 |
| 15-44 | 23972387 | 1799 | 7,5 |
| 45-64 | 17396991 | 6811 | 39,2 |
| 65-74 | 7377042 | 5479 | 74,3 |
| 75+ | 6373536 | 8241 | 129,3 |
| Total | 67063703 | 22411 | 33,4 |
Même si, individuellement, ce risque est difficile à appréhender…
Si j’ai 30 ans, au 31 mars 2020, j’ai autour de 8 chances sur 100000 d’être actuellement hospitalisé. Genre je ne me suis pas rendu compte que le taxi n’avait pas la bonne couleur.
On peut quand même tirer des conclusions plus rationnelles et utiles que précédemment :
- Les enfants sont les moins touchés (mais leur risque n’est pas nul),
- À partir de 45 ans, le risque est multiplié par plus de 5,
- À partir de 65 ans, il est ensuite multiplié par presque 2,
- Après 75 ans, il est encore multiplié par presque 2, les aînés ont 17 fois plus de risque d’hospitalisation que les jeunes (moins de 45 ans).
J’ai fait ici des calculs simples (voir trop simples) car je n’ai pris que le nombre d’hospitalisations brute et actuel, sans compter les hospitalisations terminées (retour au domicile ou décès).
Exemples possibles
Maintenant que vous avez saisi l’idée que pour inverser la condition, il faut inférer ou diviser par la bonne population, on va pouvoir utiliser les autres données.
Hospitalisations par région
Si vos craintes sont plutôt liées à votre voisinage, vous pourriez regarder les autres lignes de ce tableau qui donnent les chiffres par région. Encore une fois, les valeurs absolues et les proportions ne nous aident pas vraiment…
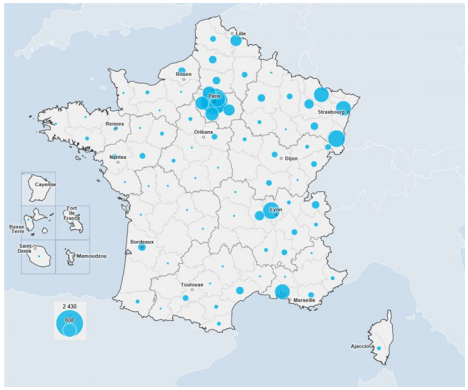
Pour calculer le risque d’être hospitalisé sachant la région dont on vient, il faut diviser le nombre d’hospitalisations par la population de la région (donnée disponible via l’INSEE), ce qui nous fournira l’incidence du virus dans la région.
Sans plus attendre, voici le tableau correspondant avec la population, les hospitalisations et l’incidence.
| Population | Hospitalisations | Incidence | |
|---|---|---|---|
| Auvergne Rhône Alpes | 8032377 | 2487 | 30,96 |
| Bourgogne Franche Comté | 2783039 | 914 | 32,84 |
| Bretagne | 3340379 | 299 | 8,95 |
| Centre Val de Loire | 2559073 | 503 | 19,66 |
| Corse | 344679 | 99 | 28,72 |
| Grand Est | 5511747 | 4246 | 77,04 |
| Hauts de France | 5962662 | 1464 | 24,55 |
| Île de France | 12278210 | 8615 | 70,16 |
| Normandie | 3303500 | 535 | 16,19 |
| Nouvelle Aquitaine | 5999982 | 672 | 11,20 |
| Occitanie | 5924858 | 874 | 14,75 |
| Pays de la Loire | 3801797 | 510 | 13,41 |
| Provence Alpes Côté d'Azur | 5055651 | 1296 | 25,63 |
Premier exemple, la Corse. En proportion, ses 99 hospitalisations comptent pour moins d’un pourcent, ce qui pourrait faire croire qu’elle est épargnée. Ramené à la population de l’île, c’est presque 30/100000. Si on part sur la moyenne nationale de 300 lits en réanimation pour 100 000 habitants, c’est 10% d’occupation, sans compter les autres pathologies qui ne respectent pas le confinement à la maison, elles.
Deuxième exemple, le Grand Est vs l’Île de France. Le nombre de cas, en absolut et proportion est plus grand dans la capitale, mais si on regarde l’incidence, c’est l’inverse. Le Grand Est est donc bien plus touché que la capitale, ce qui explique que l’hôpital militaire ait été déployé à côté de Mulhouse et pas dans la jardins du Louvre.
Si vous comparez la destination des TGV médicalisés et les incidences des régions, vous comprenez mieux le choix des destinations : privilégier les régions où les hôpitaux ont encore de la marge.
Mortalité par région
Vous pourriez aussi vous dire qu’une hospitalisation ne signifie pas la mort et que beaucoup s’en sortent après un passage à l’hôpital…
D’après les témoignage que j’ai reçu, c’est déjà pas drôle d’être malade du COVID-19 à la maison, je me dit qu’une hospitalisation, si ça peut être évité, c’est toujours ça de gagné. Mais bon, si vous vous croyez fort, les chiffres suivants vous montreront que c’est pas forcément joyeux quand même.
Dans ce cas, vous pourriez regarder les décès par région. Ici encore, la proportion ne vous sera pas d’une grande utilité puisque ce qu’on veut, c’est l’inverse…
Je n’ai pas trouvé utile de diviser cette information par la population de la région car elle ne nous dira pas grand chose d’utile tant les nombres seront faibles. Par contre, on peut calculer des chances de survie en comparant le nombre de décès et les hospitalisations :
- En divisant par le nombre de retours et de décès , qui nous donne une borne supérieure (car les décès surviennent plus rapidement que les rémissions),
- En divisant par le nombre total d’hospitalisations (en cours, décès et retours au domicile), qui nous donne une borne inférieure, car certaines hospitalisations en cours se finiront mal.
| Hospitalisations | Retours | Décès | Inf | Sup | |
|---|---|---|---|---|---|
| Auvergne Rhône Alpes | 2487 | 982 | 295 | 7,84 % | 23,10 % |
| Bourgogne Franche Comté | 914 | 675 | 214 | 11,87 % | 24,07 % |
| Bretagne | 299 | 187 | 50 | 9,33 % | 21,10 % |
| Centre Val de Loire | 503 | 113 | 60 | 8,88 % | 34,68 % |
| Corse | 99 | 100 | 20 | 9,13 % | 16,67 % |
| Grand Est | 4246 | 1704 | 1015 | 14,57 % | 37,33 % |
| Hauts de France | 1464 | 628 | 280 | 11,80 % | 30,84 % |
| Ile de France | 8615 | 2907 | 1176 | 9,26 % | 28,80 % |
| Normandie | 535 | 151 | 62 | 8,29 % | 29,11 % |
| Nouvelle Aquitaine | 672 | 348 | 78 | 7,10 % | 18,31 % |
| Occitanie | 874 | 446 | 91 | 6,45 % | 16,95 % |
| Pays de la Loire | 510 | 256 | 71 | 8,48 % | 21,71 % |
| Provence Alpes Côté d'Azur | 1296 | 897 | 103 | 4,49 % | 10,30 % |
Même si ces intervalles de mortalités sont très larges, ils permettent de voir des disparités entre régions. PACA vs la Corse par exemple. La première a près de 8 fois plus de retour et 5 fois plus de décès que la Corse, mais comme son nombre d’hospitalisation est 10 fois plus important, les taux de mortalités y sont plus faibles.
Le Grant Est est, encore une fois, le plus touché avec les taux les plus importants. Si vous n’en étiez pas déjà convaincu, c’est donc bien la région la plus touchée par le virus du COVID-19.
Mortalité par âges
Toujours dans une optique de risque individuel, on pourrait vouloir connaître la mortalité par âge. Cette fois, on va regarder les autres colonnes de ce même tableau et faire des calculs équivalents. Encore une fois, les proportions ne nous servent à rien.
| Age | Hospitalisations | Retours | Décès | Inf. | sup. |
|---|---|---|---|---|---|
| 0-14 | 81 | 228 | 0 | 0,00 % | 0,00 % |
| 15-44 | 1799 | 2340 | 29 | 0,70 % | 1,22 % |
| 45-64 | 6811 | 3395 | 319 | 3,03 % | 8,59 % |
| 65-74 | 5479 | 1609 | 589 | 7,67 % | 26,80 % |
| 75 | 8241 | 1744 | 2539 | 20,27 % | 59,28 % |
| Global | 22411 | 9316 | 3476 | 9,87 % | 27,17 % |
C’est sans doute le tableau le plus déprimant de tous car une fois hospitalisé, les chances de retour à la maison ne sont pas optimistes. On voit également que non seulement l’incidence du COVID-19 augmente avec l’âge, mais la mortalité aussi. Nos aînés sont donc doublement pénalisés.
Exemples impossibles
De nombreux autres tableaux nous fournissent des décomptes ainsi que des proportions qui sont, comme toujours, inutiles pour estimer un risque. Le problème, c’est que pour ces tableaux, on ne dispose pas de décompte de la population correspondante.
Les EHPAD (page 5). Nous donne le nombre de cas et décès survenus en EHPAD mais sans disposer du nombre total de résidents, on ne peut en calculer l’incidence. Au mieux, on peut en estimer la mortalité (8% des cas recensés sont décédés).
Comorbidité (page 9). Nous donne la proportion de cas graves avec comorbidité vs sans. Comme on ne connaît pas cette répartition dans la population générale, on ne peut inférer de risque individuel.
Cas asymptomatiques ou non graves. Le point épidémiologique ne permet pas de savoir le nombre de cas (on peut connaître les consultations, les urgences et autres mais sans savoir si ces populations sont inclues les unes dans les autres ou disjointe). On ne peut donc pas calculer l’incidence du nombre de cas ni les probabilités d’aggravation (i.e. hospitalisation sachant qu’on est positif).
Limites de l’inférence
L’Inférence Bayésienne devient vraiment intéressante lorsqu’on chaîne ces calculs à l’issue de plusieurs expériences ou mesures. Chaque événement venant apporter de plus en plus d’information nous permet ainsi d’affiner de plus en plus nos estimations de la probabilité d’une hypothèse.
Mathématiquement : Si on dispose de plusieurs observations indépendantes les unes des autres, on peut chaîner l’inférence avec des multiplications successives :
Mais pour que ça marche, il faut que les événements soient indépendant les uns des autres. S’il existe une corrélation entre eux, un facteur d’erreur apparaît. Comme ces erreurs se multiplient, le résultat s’éloigne d’autant de la réalité. L’objectif de l’inférence en est contrecarré.
Vous pourriez être tentés d’utiliser ces multiplications pour inférer un risque individualisé, en tenant compte du sexe, de l’âge, de la région, du groupe sanguin,… Mais comme beaucoup de ces caractéristiques ne sont pas indépendantes (i.e. la non symétrie de la pyramide des âges).
Il faut également compter sur les limitations des données recueillies. L’épidémie étant en cours, le calcul du taux de mortalité fourni un intervalle trop large pour avoir une réelle valeur prédictive. De même, le décompte des cas et décès ne pouvant pas être exact, l’incertitude sur ces chiffres induit une incertitude sur les probabilités calculées.
Dommage parce que ça aurait fait une chouette application 😉.
Et après ?
En toute franchise, je n’ai qu’un seul conseil à vous donner : rester prudents. Que ce soit dans la vraie vie pour réduire la propagation, que dans le monde virtuel en vérifiant toujours ce que vous lisez. Sans parler des fake news, les biais cognitifs ne sont jamais loin et il faut rester concentré pour les éviter, l’erreur arrive même aux meilleurs.
- COVID-19, Jeux du Chaos
-
16 Avril 2020 Dans une vie précédente, j'ai eu l'occasion de tracer des figures fractales à base d'ADN. C'était passionnant et je me suis demandé ce que ça donnerait avec le génome du COVID-19 qui nous empêche de sortir de chez nous.
- COVID-19, les arsouyes en quarantaine
-
13 Mars 2020 Une fois qu'on se penche sur les données scientifiques autour de la pandémie du COVID-19, on ne peut que constater son inéluctabilité et l'importance de prendre des mesures rapidement pour freiner sa propagation et sauver des vies.